Kunci Jawaban Matematika Kelas 7 Halaman 294 – 300 – Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 7 Semester 1 Halaman 294 – 300 Bab 4 Persamaan Dan Pertidaksamaan Linear Satu Variabel Uji Kompetensi 4 Hal 294 – 300 Nomor 1 – 20 PG dan 1 – 15 Uraian. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 7 di semester 1 halaman 294 – 300.
Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 7 dapat menyelesaikan tugas Persamaan Dan Pertidaksamaan Linear Satu Variabel Matematika Kelas 7 Semester 1 Halaman 294 – 300 yang diberikan oleh bapak ibu/guru.
DAFTAR ISI :
Kunci Jawaban Matematika Kelas 7 Halaman 294 – 300 Uji Kompetensi 4
A. Pilihan Ganda Hal 294 – 298
- B. 2
- A. −9
- D. 9
- D. 30
- B. -1
- C. 10
- C. 74°
- B. 40
- D. −14
- B. 59
- B. 25
- A. 5z + 30 ≤ 100
- B.
- D. −1
- C. 7 g
- D. 0 < x ≤ 6
- B. x ≤ 6
- D. 10 meter
- B. Rp20.000.000
- D. 76
B. Soal Uraian Hal 298 – 300
1. Tentukan selesaian dari persamaan berikut!
Jawaban :
a) 3y + 15 = 5y – 1
15 + 1 = 5y – 3y
2y = 16
y = 8
Jadi, nilai y adalah 8.
b) (3a + 18) / 4 = (10a – 2) / 3
3(3a + 18) = 4(10a – 2)
9a + 54 = 40a – 8
54 + 8 = 40a – 9a
31a = 62
a = 2
Jadi, nilai a adalah 2.
2. Jika b adalah bilangan asli, tentukan himpunan selesaian persamaan!
Jawaban :
2 + 11/b = 7 1/2
11/b = 15/2 – 4/2
11/b = 11/2
11b = 22
b = 2
Jadi, nilai b adalah 2.
3. Jika 3x + 12 = 6x − 18, tentukanlah nilai dari x − 2.
Jawaban :
3x + 12 = 6x – 18
6x – 3x = 12 + 18
3x = 30
x = 10
x – 2 = 10 – 2 = 8
Jadi, nilai x – 2 adalah 8.
4. Pak Ali berumur 28 tahun, ketika anaknya lahir. Berapakah umur Pak Ali ketika umur anak tersebut 16 tahun?
Jawaban :
Umur Pak Ali = 28 + 16 = 44
Jadi, umur Pak Ali ketika anaknya berumur 16 tahun adalah 44 tahun.
5. Diketahui harga sepasang sepatu sama dengan dua kali harga sepasang sandal. Pak Syakir membeli 4 pasang sepatu dan 3 pasang sandal.
Jawaban :
Misal sepatu = x, dan sendal = y
x = 2y
4x + 3y = 385000
4(2y) + 3y = 385000
11y = 385000
y = 35000
x = 2y
x = 2(35000)
x = 70000
Jadi, harga sepasang sepatu adalah Rp.70.000.
6. Suatu setigita sama kaki memiliki panjang kaki sama dengan 5 kali panjang sisi lainnya.
Jawaban :
5x + 5x + x > 55
11x > 55
x > 55/11
x > 5
Jadi, panjang minimum masing-masing sisi segitiga tersebut adalah 6m, 30m, dan 30m.
7. Pak Ketut berencana akan membangun rumah di atas sebidang tanah berbentuk persegipanjang dengan ukuran panjang 30 m dan lebar (2y + 1) m.
Jawaban :
a) luas ≥ p x l
150 ≥ 30 x (2y + 1)
150 ≥ 60y + 30
120 ≥ 60y
2 ≥ y
2(2) + 1 = 5
Jadi, lebar maksimum tanah Pak Ketut adalah 5m.
b) Biaya maksimal = luas maximal x biaya
= 150 x 4.500.000
= 675.000.000
Jadi, biaya maksimal yang harus disediakan pak Ketut adalah Rp.675.000.000.
8. Pak Todung memiliki sebuah mobil box pengangkut barang dengan daya angkut maksimal 1 ton.
Jawaban :
a) Banyak kotak sekali angkut = (daya angkut – berat Pak Todung) / berat tiap kotak
= (1000 – 50) / 25
= 950 / 25
= 38 Kotak
b) Banyak pengangkutan = banyak kotak / banyak kotak sekali angkut
= 1994 / 38
= 53 Pengangkutan
c) Banyak kotak sekali angkut = (daya angkut – berat Pak Todung) / berat tiap kotak
= (1000 – 50) / 50
= 950 / 50
= 19 Kotak
9. Tentukan selesaian dari pertaksamaan berikut!
Jawaban :
a) 2x -6 ≥ 8x + 5
2x – 8x ≥ 5 + 6
-6x ≥ 11
x ≤ -11/6
b) 1/2x + 5 > 15
1/2x > 15 – 5
1/2x > 10
x > 10 x 2/1
x > 20
c) 2/3p + 4 ≤ 8
2/3p ≤ 8 – 4
2/3p ≤ 4
p ≤ 4 x 3/2
p ≤ 6
d) (2y – 7) / 2 < 3
2y – 7 < 3 x 2
2y < 6 + 7
y < 13/2
10. Ubahlah persamaan berikut ke dalam permasalahan sehari-hari!
Jawaban :
a) 5a – 1 < 6
Diacara ulang tahun terdapat 5 kantung permen yang jumlah permen diseluruh kantung tersebut kurang dari 6, lalu seseorang mengambil 1 permen dari salah satu kantung tersebut.
b) 7 ≥ 3x
Terdapat 3 keranjang buah yang jumlah seluruh buahnya tidak lebih dari 7 buah.
11. Jumlah tiga bilangan genap berurutan adalah 126.
Jawaban :
a) Karena bilangan genap maka setiap + 2 hasilnya selalu genap.
2n + (2n + 2) + (2n + 4) = 126
6n + 6 = 126
6n = 120
n = 20
Bilangan pertama = 2n = 2(20) 40
Bilangan kedua = 2n + 2 = 2(20) + 2 = 42
Bilangan ketiga = 2n + 4 = 2(20) + 2 = 44
Jadi, bilangan genap kedua dan ketiga adalah 42 dan 44.
12. Nilai x pada gambar berikut adalah
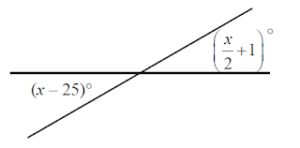
Jawaban :
x – 25 = x/2 + 1
x – x/2 = 1 + 25
x/2 = 26
x = 52°
Jadi, nilai x pada gambar tersebut adalah 52°.
13. Diberikan batasan nilai x dan y, yaitu 3 ≤ x ≤ 25 dan −9 ≤ y ≤ −1. Carilah nilai terbesar dari
Jawaban :
a) Untuk mendapatkan nilai terbesar maka x harus maximal dan y harus minimal, didapat x = 25 dan y = -9
3x – 9y = 3(25) – 9(-9)
= 75 + 81
= 156
Jadi, terbesar dari 3x – 9y adalah 156.
b) Untuk mendaptkan nilai terkecil maka y harus minimal dan x harus maximal, didapat y = -9 dan x = 25
2y/x + x/y = 2(-9)/25 + 25/(-9)
= -18/25 + 25/-9
= 787/-225
= -3,5
14. Panjang diagonal belah ketupat adalah (3x − 2) cm dan (x + 14) cm.
Jawaban :
3x – 2 > x + 14
3x – x > 14 + 2
2x > 16
x > 8
15. Sepotong kawat yang panjangnya 196 m dibentuk menjadi suatu kerangka balok.
Jawaban :
a) Panjang kawat ≥ 4 x (p + l + t)
196 ≥ 4 x (5x + 3 + 4x – 2 + x – 2)
196 ≥ 4 x (10x -1)
196 ≥ 40x – 4
200 ≥ 40x
5 ≥ x
b) Nilai x maksimum adalah 5
c) panjang = (5x + 3) = 5(5) + 3 = 28
lebar = (4x – 2) = 4(5) – 2 = 18
tinggi = (x – 2) = 5 – 2 = 3
Itulah dia pembahasan dan Kunci Jawaban Matematika Kelas 7 Semester 1 Halaman 294 – 300 Bab 4 Persamaan Dan Pertidaksamaan Linear Satu Variabel Uji Kompetensi 4 Hal 294 – 300 Nomor 1 – 20 PG dan 1 – 15 Uraian, semoga bermanfaat untuk adik – adik semua. Jika ada yang belum jelas bisa ditanyakan di kolom komentar Gudangjawaban.com.
