Trigonometri: Rumus, Turunan, Tabel, & Contoh Soal – Materi trigonometri merupakan salah satu materi matematika yang membutuhkan pemahaman lebih dalam. Seringkali soal yang menyangkut trigonometri merupakan gabungan dari beberapa rumus trigonometri. Berikut ini beberapa rumus yang digunakan dalam trigonometri beserta dengan soal dan pembahasannya.
DAFTAR ISI :
Pengertian Trigonometri
Trigonometri adalah materi segitiga yang berfokus pada kesebangunan segitiga siku-siku dan sisi-sisi yang bersesuaian pada dua bangun segitiga yang memiliki perbandingan yang sama. Sebagian besar trigonometri berfokus pada sudut-sudut yang membentuk segitiga beserta dengan kuadran sudut yang dihasilkan.
Hubungan antara sudut-sudut dalam segitiga membentuk 3 buah sisi yaitu sisi samping, sisi depan, dan sisi miring. Sisi depan dan sisi samping bergantung terhadap letak sudut yang digunakan sebagai acuan. Untuk lebih jelasnya bisa melihat gambar di bawah ini untuk membedakan sudut samping dan sudut depan.
Rumus Trigonometri
Setelah kamu mengetahui sudut dan sisi yang menjadi dasarnya, berikut ini beberapa rumus yang biasa digunakan.
1. Aturan Sinus
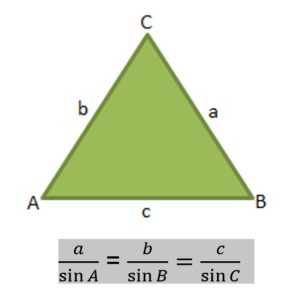
2. Aturan Cosinus
- BC2 = AC2 + AB2 – (2ACAB) cos A)
- AC2 = BC2 + AB2 – (2ABAC cos B)
- AB2 = AC2 + BC2 – (2ACBC cos C)
3. Aturan Tangen
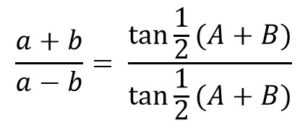
4. Rumus Fungsi Dasar Trigonometri

5. Rumus Identitas
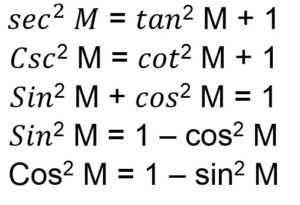
6. Rumus Jumlah dan Selisih Sudut pada Trigonometri
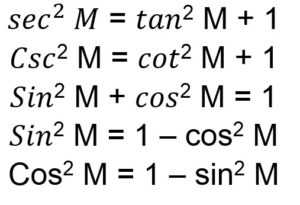
7. Rumus Perkalian
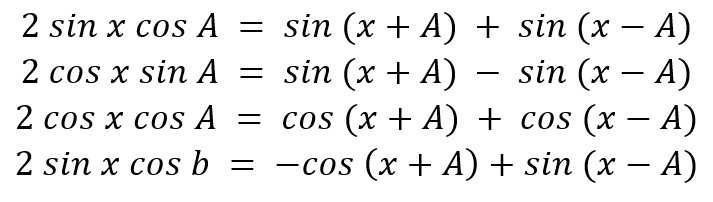
8. Rumus Jumlah dan Selisih
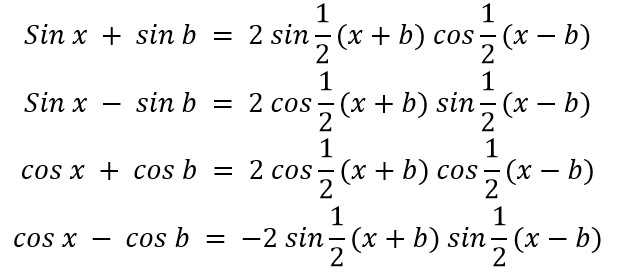
9. Rumus Sudut Rangkap Dua dan Tiga
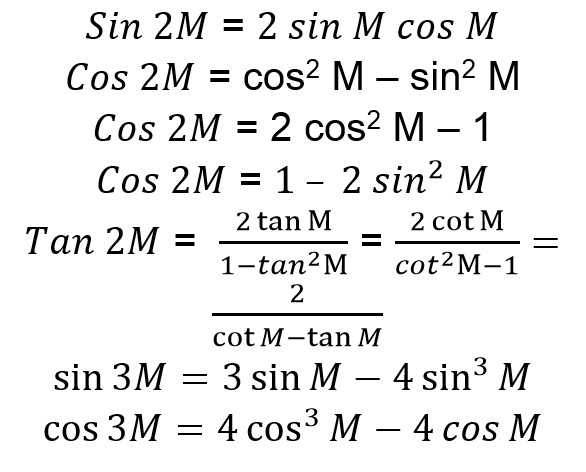
10. Rumus Setengah Sudut
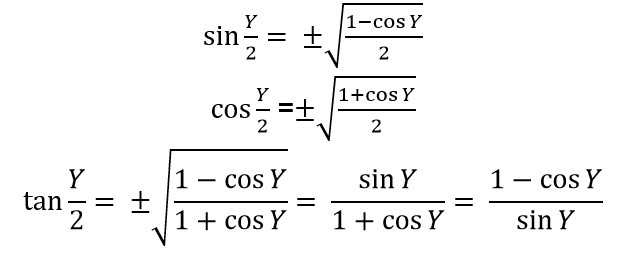
Contoh Soal dan Pembahasan Trigonometri
Berikut ini contoh soal, pembahasan dan kunci jawaban mengenai materi Trigonometri yang bisa adik – adik pelajari.
1. Berapakah hasil dari 2 sin 75o cos 15o
Untuk mengerjakan soal di atas, kamu harus mengingat rumus trigonometri kembali. Dari banyak rumus trigonometri yang diberikan, bentuk di atas bisa menggunakan rumus trigonometri seperti di bawah ini.
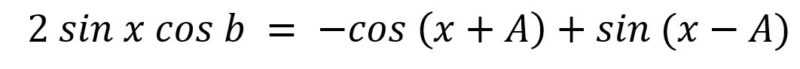
Sehingga kamu bisa mengubah soal menjadi bentuk rumus di atas.
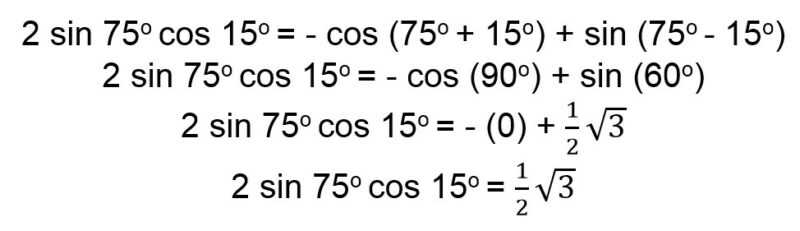
2. Berapakah hasil dari sin 105o – sin 15o
Untuk mengerjakan soal di atas, kamu bisa melihat kembali rumus yang ini dapat kalian gunakan. Dikarenakan bentuk tersebut ada penjumlahan sudut, maka kamu bisa menggunakan rumus berikut ini.
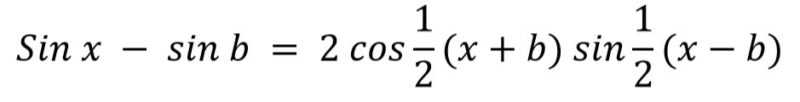
Sehingga kamu bisa mengubah bentuk soal ke dalam bentuk rumus tersebut.

3. Jika diketahui nilai tan A = , maka tentukan hasil dari
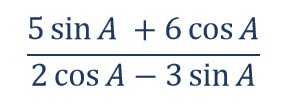
Untuk mengerjakan soal di atas, kamu harus memahami bentuk dari tan A terlebih dahulu seperti di bawah ini.
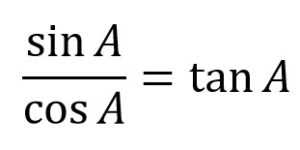
Setelah kamu mengerti bentuk tan A, maka kamu bisa mengubah bentuk trigonometri soal dengan mengubahnya menjadi tan A dengan cara mengalikan pembilang dan penyebutnya dengan cos A seperti di bawah ini. =
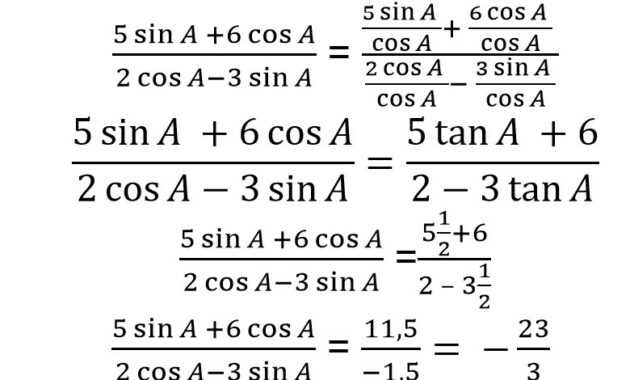
4. Diketahui sebuah nilai tan B = , jika tan B berada di kuadran I, berapakah hasil
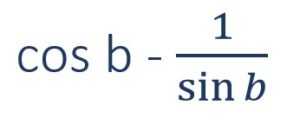
Untuk mengerjakan soal tersebut, kamu harus menulis kembali informasi yang ada di dalam soal.
- Sudut B berada di Kuadran I
- tan B = 1/b
Dari informasi di atas, kamu bisa mengingat sifat tan dalam segitiga. Tan adalah perbandingan antara sisi depan segitiga dengan sisi samping segitiga. Untuk lebih jelasnya, kamu bisa melihat gambar di bawah ini. Sehingga kamu bisa menuliskan bentuk tan B menjadi seperti di bawah ini.
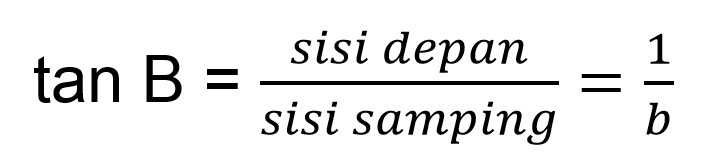
Dari bentuk di atas, kamu bisa berasumsi bahwa panjang sisi depan = 1 dan panjang sisi samping = b. Sehingga kamu bisa mencari panjang sisi miring dengan rumus phytagoras.
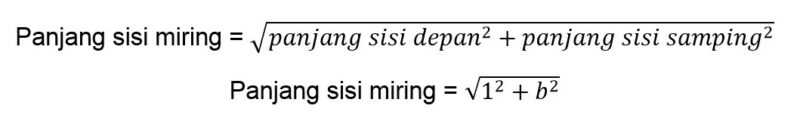
Kamu bisa mengerjakan soal di atas dengan mengubah bentuknya menjadi persamaan panjang segitiga.
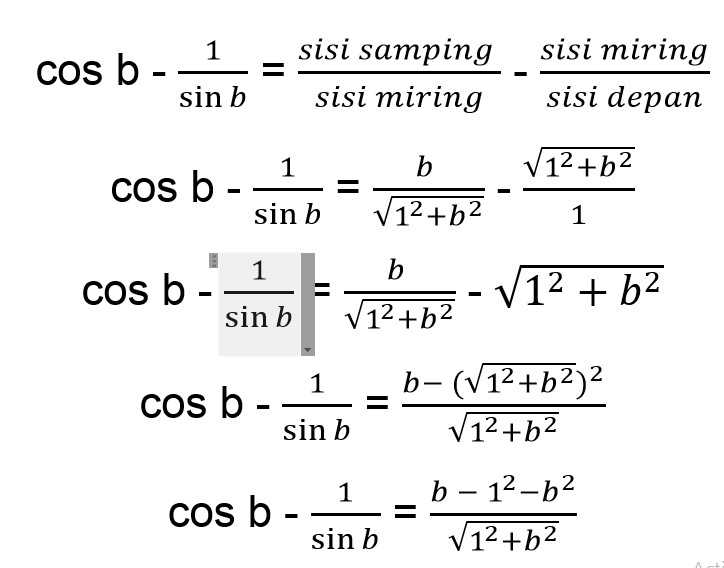
Sehingga bentuk akhir dari soal di atas adalah:
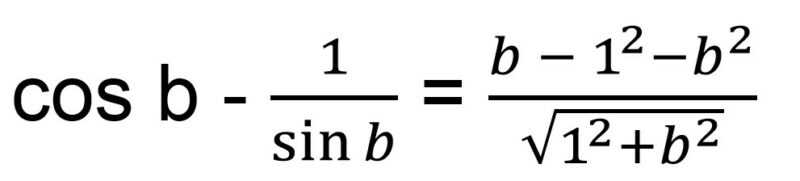
Setelah mempelajari soal trigonometri di atas, kamu akan melihat bahwa rumus trigonometri dapat digunakan secara kombinasi dengan rumus lainnya untuk menyelesaikan soal tersebut. Sehingga belajar mengerjakan banyak soal dapat membantumu meningkatkan pemahaman dan kecakapan dalam mengerjakan soal trigonometri.
Itulah dia beberapa rumus yang digunakan dalam trigonometri beserta dengan soal dan pembahasannya. Semoga materi pendidikan ini bermanfaat untuk adik adik semuanya, jika ada yang belum paham bisa ditanyakan di kolom komentar GudangJawaban.com.

